UNICIENCIA Vol. 30, No. 1, pp. 1-16. Enero-Junio, 2016.
URL: www.revistas.una.ac.cr/uniciencia
Email: revistauniciencia@una.cr
ISSN Electrónico: 2215-3470
DOI: http://dx.doi.org/10.15359/ru.30-1.1
Conocimiento común del contenido que manifiesta un profesor al enseñar los conceptos básicos de funciones: un estudio de caso
Common Content Knowledge manifested by a teacher in teaching basic concepts of functions: A case study
Ariana Rodríguez-Flores
Universidad Nacional
Heredia, Costa Rica
Miguel Picado-Alfaro
Universidad Nacional
Heredia, Costa Rica
Jonathan Espinoza-González
Universidad Nacional
Heredia, Costa Rica
Nielka Rojas-González
Universidad Católica del Norte
Antofagasta, Chile
Pablo Flores-Martínez
Universidad de Granada
Granada, España
Recibido-Received: 4/mar/2015 / Aceptado-Accepted: 26/jun/2015 / Publicado-Published: 31/ene /2016.
Resumen
Este artículo presenta un estudio de caso sobre el conocimiento común del contenido matemático que manifiesta un profesor al enseñar los conceptos básicos de función en un colegio académico diurno de Educación Secundaria de Costa Rica. Se basa en las investigaciones sobre el conocimiento matemático para la enseñanza que es una línea de investigación en auge en la formación del profesado. Se utiliza el análisis didáctico como herramienta para identificar y caracterizar este conocimiento. Identificamos que el profesor exterioriza un conocimiento significativo de conceptos matemáticos, de conocimiento procedimental apropiado y una capacidad valiosa para definir estructuras conceptuales, asimismo este saber se relaciona con el conocimiento del programa de estudios para educación secundaria, indicadores que se entrelazan con el conocimiento didáctico del contenido.
Palabras claves: Docente de secundaria, enseñanza de las matemáticas, formación de docentes de secundaria, matemáticas.
Abstract
This article presents a case study based on the common knowledge of the content in mathematics shown by a professor when teaching basic function concepts in a daytime academic high-school in Costa Rica. It is based on research regarding the mathematics knowledge required for teaching, which is a booming research area in faculty training. The educational analysis is used as a tool to identify and characterize this knowledge. We recognize that the professor shows significant knowledge of mathematical concepts, appropriate procedural knowledge and valuable ability to define conceptual structures. Furthermore, this knowledge relates to knowing about the study program for high-school education, indicators which intertwine with the educational knowledge of the content.
Keywords: Mathematics; Mathematics education; Secondary school teachers; Secondary teacher education.
Desde un marco general, el personal docente constituye uno de los agentes claves en los procesos de enseñanza y aprendizaje de las matemáticas. Comúnmente, se reconoce en el profesorado la responsabilidad de mediar pedagógicamente en este proceso. Como participante de estos procesos, debe guiar al estudiantado en la construcción del conocimiento (Salcedo, 2012) y orientar el desarrollo del pensamiento crítico y reflexivo (Badilla, Chavez, Herrera, Morales, Poveda, Román y Sánchez, 2004). Además, más allá de un componente didáctico, el profesor debe ser experto en matemáticas, es decir, tener conocimientos matemáticos profundos para enseñar.
Estudiar el conocimiento profesional del docente de matemáticas es un tema (o problema) presente en la agenda de los investigadores en la línea de formación de profesores y profesoras. En las últimas décadas, se han realizado esfuerzos para analizar distintas particularidades del conocimiento matemático y pedagógico del profesorado que permitan caracterizar este conocimiento y teorizar sobre la práctica docente.
Recientemente, diversas evaluaciones han señalado las dificultades y el bajo rendimiento de estudiantes de educación secundaria en matemáticas en Costa Rica (Ministerio de Educación Pública de Costa Rica [MEP], 2012). Con especificidad, las funciones forman parte de uno de los temas que muestran un menor porcentaje de aprobación entre estudiantes. Este fenómeno se extiende a profesores de matemáticas, quienes manifiestan un déficit en el conocimiento del contenido matemático que podría estar incidiendo en el proceso de enseñanza y aprendizaje de las matemáticas (Cuarto Informe Estado de la Educación, 2013).
Ante este panorama, interesa estudiar el conocimiento matemático del profesorado. En este trabajo nos centraremos en discutir el subdominio del Conocimiento Común del Contenido (CCC), que es uno de los seis subdominios de conocimiento del modelo MKT, correspondiente al Conocimiento Matemático para la Enseñanza propuesto por Ball, Thames y Phelps (2008). Nos interesa mostrar resultados del subdominio CCC, ya que es uno de los subdominios que más se destaca en el análisis del conocimiento del docente, sujeto informante de esta investigación. Consideramos que comprender el CCC del profesor nos puede permitir profundizar el conocimiento de la enseñanza que manifiesta el docente.
Presentamos los resultados de un estudio de caso sobre el CCC que manifiesta un profesor de matemáticas que enseña el tema de funciones a estudiantes entre 16-17 años de edad en Costa Rica. Este estudio tiene como objetivo caracterizar el CCC de un profesor de matemáticas al enseñar los conceptos básicos de función en cuarto nivel de la educación secundaria, en un colegio académico diurno en la provincia de Heredia. Para su consecución se han definido tres objetivos específicos.
- Describir el proceso de enseñanza que sigue un profesor de matemática al enseñar los conceptos básicos de función.
- Identificar los componentes del conocimiento del contenido que manifiesta un profesor de matemática al enseñar los conceptos básicos de función.
- Determinar indicadores sobre el conocimiento del contenido que caracterizan a un profesor de matemática que enseña los conceptos básicos de función.
Marco teórico
Diversas investigaciones han abordado el conocimiento matemático para la enseñanza centrándose en estudiar distintos subdominios de conocimiento que organizan los saberes necesarios para enseñar matemáticas. Por ejemplo, Ball, Thames y Phelps (2008) categorizan el conocimiento del profesor de matemáticas en seis subdominios de conocimiento. Considerando el conocimiento matemático del profesorado para la enseñanza como “el conocimiento matemático que los profesores utilizan en el aula para producir aprendizaje y crecimiento en los alumnos” (Hill, Ball y Schilling, 2008, p.374). Así, cada docente debe poseer un conocimiento específico para la enseñanza que va más allá del conocimiento matemático.
Carrillo, Climent, Contreras y Muñoz-Catalán (2013) presentan un modelo analítico para el estudio del conocimiento del profesor de matemáticas, denominado Mathematics Teacher’s Specialised Knowledge (MTSK). Este modelo asigna un carácter especializado al conocimiento del profesorado, permitiendo a su vez interpretar el conocimiento especializado del docente de matemáticas desde un punto de vista integral, considerando la naturaleza diferente del dominio matemático y del dominio pedagógico del contenido matemático. Los modelos de conocimiento que surgen en la literatura han permitido, a quienes investigan, comprender, en profundidad, el conocimiento que manifiestan docentes en su práctica. Por ejemplo, Rojas (2010, 2014) estudia el conocimiento especializado que manifiestan profesores expertos al enseñar el tema de las fracciones; Carmona y Climent (2012) analizan el conocimiento de un profesor al enseñar ecuaciones de una recta.
Consideramos que estudiar el conocimiento que presentan docentes de matemática en su práctica aporta información sobre la naturaleza de los subdominios de conocimiento y permite identificar indicadores precisos de conocimiento a partir de la actuación docente.
El Conocimiento Profesional del profesor se entiende como aquellos saberes y experiencias que pone en su práctica docente, que viene construyendo desde su formación inicial y durante el desarrollo de su carrera (Climent, 2002).
Esta investigación se centrará en la experiencia del profesor participante como el medio de la construcción del conocimiento profesional. Interesa, en particular, comprender el conocimiento elemental que este profesor emplea para enseñar las funciones.
Considerando las ideas de Shulman (1986, 1987) el profesor debe ser capaz de manejar las definiciones y poder justificar proposiciones en particular, así como conocer cómo se relaciona el conocimiento con otras disciplinas. El profesor debe analizar la forma de presentar la materia al estudiante; debe tomar en cuenta las habilidades y dificultades que puedan presentar, además de adaptarla a la diversidad de interés de los jóvenes, entre otros aspectos. Entendemos que estudiar el conglomerado de conocimiento que un profesor pone en juego al enseñar un contenido es un tema amplio, por lo cual nos vamos a centrar, como mencionamos anteriormente, en comprender el conocimiento elemental que un profesor exterioriza al enseñar el tema de las funciones.
Empleamos el modelo de Conocimiento Matemático para la Enseñanza (MKT) propuesto por Ball, Thames y Phelps (2008), que distingue el Conocimiento del Contenido y Conocimiento Pedagógico del Contenido. La figura 1 muestra el modelo propuesto por los autores.
El Conocimiento del Contenido, que enfoca las matemáticas, se compone de tres subdominios: Conocimiento Común del Contenido (CCC), Conocimiento en el Horizonte Matemático (CH) y Conocimiento Especializado del Contenido (CEC). Para este estudio solo se considerará el CCC. Este corresponde al conocimiento que adquiere una persona a través de la escuela o la vida. Godino (2009) se refiere a este conocimiento como el necesario para resolver problemas matemáticos, ya sea para una persona adulta con conocimiento suficiente o para una persona especialista en matemática. En esta categoría, el docente de matemáticas debe ser capaz de reconocer las respuestas inadecuadas de sus estudiantes, hacer uso correcto de la notación e identificar imprecisiones de definiciones propuestas en libros de texto (Gómez, 2007). Por tanto, el foco de atención está en la matemática elemental o necesaria para abordar el tema en cuestión, y nuestro foco de interés es comprender los aspectos contribuyentes del subdominio CCC.
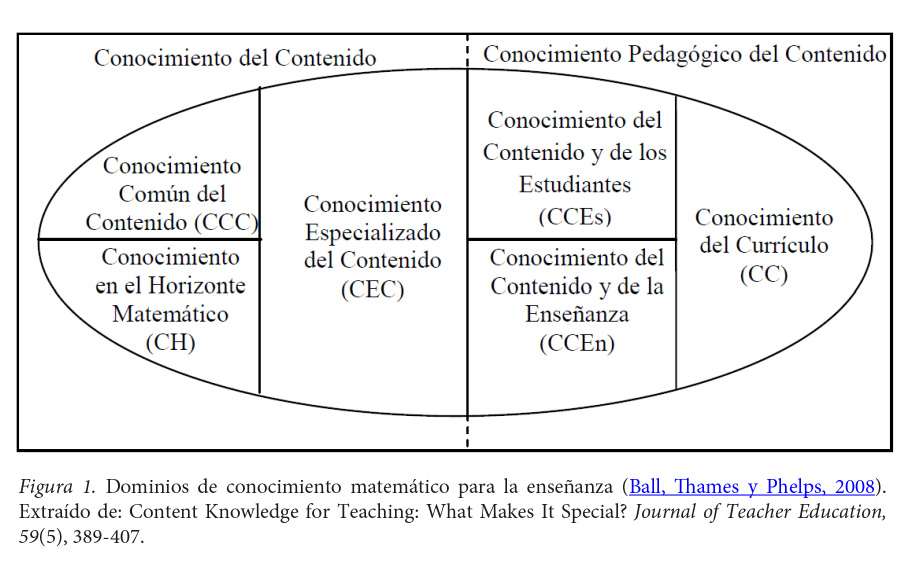
El Conocimiento Pedagógico del Contenido acentúa los procesos de enseñanza y el aprendizaje de las matemáticas. Se integra por tres subdominios: Conocimiento del Contenido y de los Estudiantes (CCE), Conocimiento del Contenido y de la Enseñanza (CCEs) y Conocimiento del Currículo (CC). Estos dominios no serán considerados en este estudio, pues el foco de atención es el Conocimiento Común del Contenido.
Análisis didáctico
En España, el Grupo de Investigación Pensamiento Numérico del Departamento de Didáctica de la Matemática de la Universidad de Granada propone el análisis didáctico como una metodología de investigación útil en los estudios sobre formación de profesores e innovación curricular. Este estudio se ubica en este marco conceptual.
Rico (1997) destaca una serie de conocimientos para diseñar, desarrollar y evaluar unidades didácticas, a los que llama organizadores del currículo. Estos componentes fundamentales de la práctica del profesorado proporcionan un marco conceptual para la enseñanza de las matemáticas, promueven la reflexión sobre los procesos de transmisión y construcción del conocimiento matemático y otorgan criterios para tratar la complejidad de estos procesos. A partir de estos organizadores se construye la base del análisis didáctico.
Gómez (2007) define el análisis didáctico como el “procedimiento con el que es posible explorar, profundizar y trabajar con los diferentes y múltiples significados del contenido matemático escolar, para efectos de diseñar, llevar a la práctica y evaluar actividades de enseñanza y aprendizaje” (pp. 18-19). Está integrado por cinco análisis parciales: (a) análisis conceptual, (b) análisis de contenido, (c) análisis cognitivo, (d) análisis de instrucción y (e) análisis de evaluación (Rico y Fernández-Cano, 2013).
El análisis conceptual indaga la variedad de significados, las posibles relaciones entre los términos, las creencias y concepciones de cada campo conceptual. Su objetivo es fundamentar y clarificar conceptos y términos. Este análisis va a sustentar la primera dimensión del análisis del contenido (Rico y Fernández-Cano, 2013). El análisis de contenido explora el significado de un concepto matemático en tres dimensiones: estructura conceptual, fenomenología y sistema de representación. El docente debe disponer de una organización del contenido para elegir las tareas que realizará en el proceso de enseñanza (Rojas, Flores y Ramos, 2013).
El análisis cognitivo se estructura en expectativas, limitaciones y oportunidades en el aprendizaje escolar (Lupiañez, 2009). Las expectativas son los fines, objetivos y capacidades para establecer caminos de aprendizaje. Las limitaciones se refieren a los errores y dificultades que tienen los estudiantes al aprender un tema. Las oportunidades muestran las tareas planteadas o propuestas para la enseñanza de un contenido. El análisis de instrucción consiste en el diseño, análisis y selección de tareas como elementos de la unidad didáctica de planificación. Analiza también instrumentos de evaluación y recursos didácticos (Lupiañez, 2009). El análisis de evaluación logra describir las habilidades y dificultades que han manifestado estudiantes durante el proceso escolar (Gómez, 2007). Este permite una evaluación de los análisis previos y su utilidad para establecer modificaciones e iniciar nuevamente el ciclo de análisis.
Rojas (2010, 2014) y Rojas, Flores y Ramos, 2013 proponen el análisis didáctico como un instrumento óptimo para identificar conocimiento matemático para la enseñanza del profesorado en la acción docente, es decir, durante la ejecución de las lecciones. Esta investigación enfoca el análisis conceptual y de contenido desde la perspectiva de estos autores.
Marco curricular
El Programa de Estudio de Matemáticas del Ministerio de Educación Pública de Costa Rica [MEP] (MEP, 2012), propone como enfoque principal la resolución de problemas en contextos reales. Este programa se implementa desde el año 2012 por medio de planes de transición. La tabla 1 muestra los conocimientos y habilidades específicas correspondientes al cuarto nivel de educación secundaria del Programa de Transición 2014.
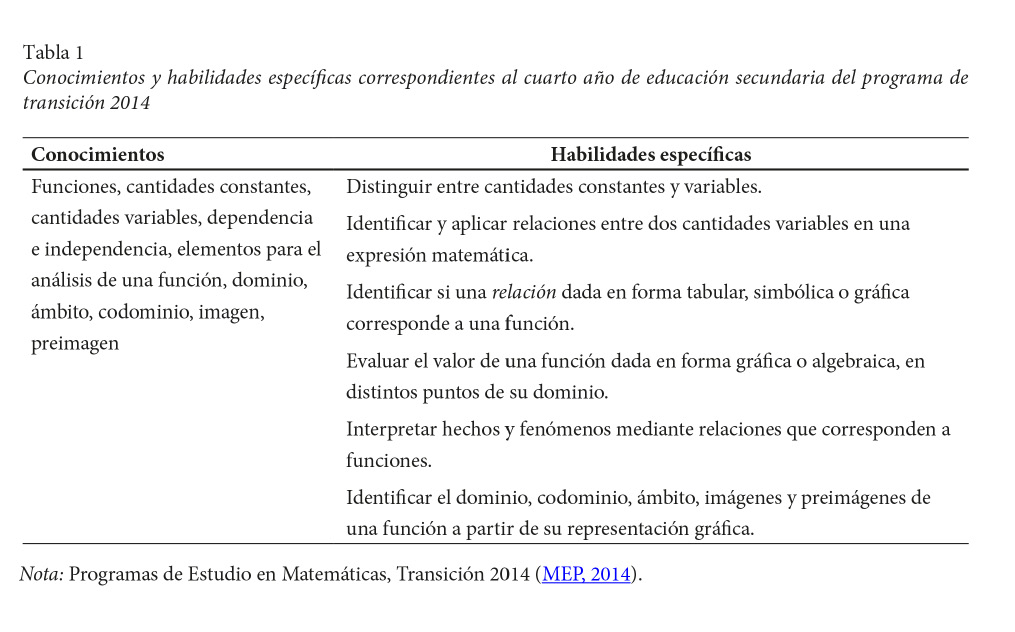
Metodología
La investigación es de carácter cualitativo basada en estudio de caso. Este tipo de investigación “utiliza un diseño de estudio de caso que significa que el análisis de los datos se centra en un fenómeno, seleccionado por quien investiga para entender independientemente del número de escenarios o de participantes en el estudio” (McMillan y Schumacher, 2005, pp. 402-403). La investigación se centra en la descripción del conocimiento común del contenido que manifiesta un profesor de matemáticas al enseñar las funciones en el ciclo diversificado, en un colegio de Costa Rica.
La fuente de información es un profesor de matemáticas de educación secundaria. Su selección responde a una serie de criterios definidos a partir de los propósitos del estudio, los planteamientos del equipo investigador del proyecto en que se enmarca esta investigación y las propuestas de investigaciones previas (Rojas, Carrillo y Flores, 2012). Estos incluyen identificar a los sujetos informantes según el contexto de estudio y la disponibilidad. También se toman como base características primarias y secundarias para seleccionar docentes con experticia, como experiencia mínima de cinco en enseñanza de las matemáticas y del tema en estudio y ser consciente del cambio curricular (Rojas, Carrillo y Flores, 2012, p.483).
Recolección de datos
Los datos se recolectaron mediante observaciones (no participantes) de clase. La información se ha registrado en grabaciones de audio y video. Esto para mantener un registro real y cercano a lo acontecido en la clase durante la fase de análisis y evitar la omisión de detalles trascendentales para los resultados del estudio.
Análisis de la información
Para analizar la información se han adaptado las categorías sobre el CCC propuestas por Rojas, Flores y Ramos (2013). Para cada categoría se establece una serie de unidades de análisis para estudiar el CCC de un profesor cuando enseña el tema de funciones. Como parte del estudio, para definir las unidades de análisis, se ha llevado a cabo el análisis didáctico de las funciones desde los principios del análisis de conceptual y de contenido. Esto ha permitido determinar la interpretación de la función como relación funcional entre magnitudes y como relación matemática unívoca. Las categorías y las unidades de análisis se muestran en la tabla 2.
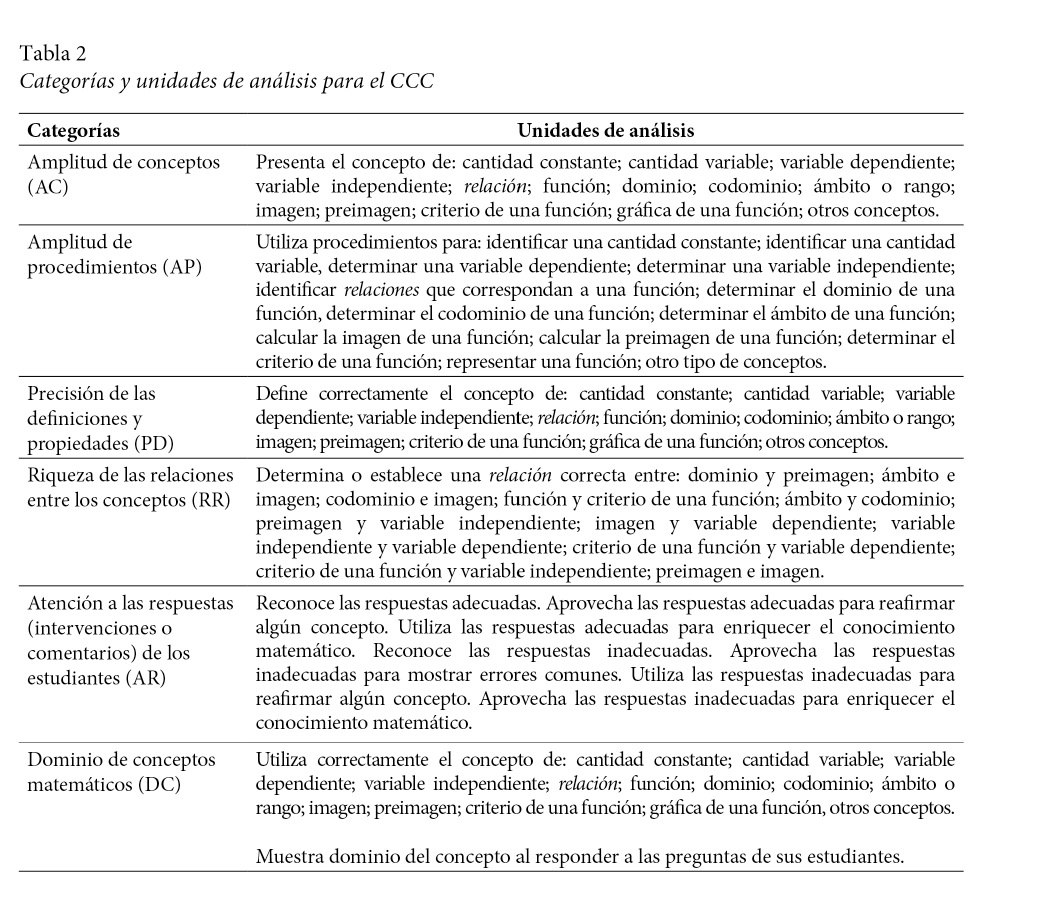
Estos indicadores han sido revisados por expertos. Su definición permite identificar en la práctica docente los rasgos sobre el CCC que manifiesta el profesor de matemáticas observado al abordar el tema en estudio.
Discusión y resultados
La información obtenida se organizó por medio de seis episodios de clases. Cada episodio corresponde a una sesión de grabación (Las sesiones de grabación pueden corresponder a una o dos lecciones de clase. En la educación secundaria en Costa Rica cada lección de clase es de 40 minutos). Luego, se hace una descripción de los episodios, que muestra una síntesis del trabajo del profesor en la clase, los conocimientos abarcados y las evidencias sobre las categorías de análisis. Los códigos AC, AP, PD, RR, AR, DC corresponden a las categorías de análisis descritas en la tabla 2.
Análisis del conocimiento común del contenido por episodio
Este apartado describe cada episodio respecto a las categorías sobre el CCC consideradas. Esta información se acompaña con fragmentos de algunas de las intervenciones grabadas durante la clase. Aquellas hechas por el profesor se identifican con P y las que corresponden a estudiantes con Ei. El subíndice se empleará para distinguir las intervenciones de estudiantes. Por ejemplo, las indicaciones E1 y E2 refieren a distintos estudiantes que dialogan con el profesor. Si se escribe la letra E (sin subíndice) es porque la intervención la realiza un grupo de estudiantes de forma simultánea.
Episodio [1]
Síntesis del episodio. El profesor presenta un problema y solicita al grupo de estudiantes que, en grupos, lo resuelvan. Luego, un estudiante de cada grupo va a la pizarra a mostrar el procedimiento y la solución encontrada. El problema trata el costo del servicio de taxi en Costa Rica tomando en consideración la tarifa básica y el kilometraje adicional; enfatiza en el cálculo del costo del servicio para distancias recorridas particulares (enteras y fraccionarias), el establecimiento de una fórmula general para este cálculo y la estimación de distancias a partir de montos de dinero disponible.
Conocimientos abarcados. Variable, variable dependiente, variable independiente, ecuación.
Análisis del episodio
La resolución del problema planteado por el profesor permite introducir la noción de nuevos conceptos [AC]. El profesor demuestra, en su explicación, el uso correcto de cada uno de los conceptos [DC].
P: De esas dos variables ¿quién depende de quién? El costo va a depender de los kilómetros adicionales que yo recorra en el taxi. Entonces, aquí vamos a decir que para la próxima lección en que ya nos vamos a meter de lleno en eso, en lo que es la definición de variables, este costo depende de los kilómetros adicionales, ¿Quiénes son los kilómetros adicionales?, x, entonces ¿C depende de quién?
E: De x
P: Entonces podemos decir que C es una variable ¿qué?, si depende ¿C es una variable?
E: Dependiente
P: Dependiente, correcto. Ahora, los kilómetros adicionales, pues C es dependiente, ¿qué pasaría con la variable x que son los kilómetros adicionales? Sería una variable ¿qué?
E: Independiente
El contenido matemático en las respuestas adecuadas e inadecuadas es utilizado para reforzar el conocimiento [AR].
P [mientras E1 escribe en la pizarra]: ¿La primera parte coincide E1?,
E1: [el estudiante mueve la cabeza indicando una negación]
P: ¿No?
E1: [el estudiante explica el procedimiento realizado y el significado de las representaciones simbólicas utilizadas, no se entiende el audio puesto que el estudiante habla en tono muy bajo]
P: Ok. Vean que tenemos una fórmula diferente a la del grupo 1, la del grupo 2 es la misma fórmula. [El estudiante sigue escribiendo en la pizarra la solución del ejercicio (parte C)]. La C difiere de la respuesta, ¿verdad?, dos mil setecientos sesenta [al comparar con la solución del grupo 1]. Por lo tanto, imagino que la D difiere también…
P: Vean que interesante la diversidad de respuestas que ustedes tienen. Se acuerdan la vez pasada también con el problema de ecuaciones cuadráticas, ustedes tenían variedad de preguntas diversas; respuestas, perdón, diversas. Ahorita lo que tenemos que llegar es llegar a una conclusión ya general que todos tengamos exactamente lo mismo. En el grupo tres hubo una diferencia entre el mismo grupo, tres personas opinaron una cosa y dos opinaron otra, no llegaron a una conciliación…
P: Ok chicos, vean. Todo lo que hicieron tiene validez. Sin embargo vamos ya a generalizar todas las situaciones [el profesor procede a resolver el problema, apoyado en preguntas que los estudiantes van respondiendo]
Episodio [2]
Síntesis del episodio. El profesor retoma el problema de la clase anterior sobre la tarifa de taxi. Utiliza el folleto (material didáctico impreso elaborado por el profesor) para exponer ejemplos, ejercicios y conceptos.
Conocimientos abarcados. Cantidad constante, cantidad variable, variable dependiente, variable independiente, relación.
Análisis del episodio
Mediante el repaso del problema de la clase anterior, el profesor introduce los primeros conceptos correspondientes al tema de funciones. Además, durante el desarrollo de la lección menciona otros conceptos sobre este tema [AC].
P: Diremos que los elementos que conforman una relación se van a denominar pares ordenados, entonces ya aquí hay un nuevo concepto, ¿qué son pares ordenados?, son aquellos elem..., son aquellas asociaciones que hacemos con los elementos de “A” y los elementos de “B”.
Sobre los procedimientos utilizados, el profesor destaca la manera para identificar una variable dependiente [AP].
P: Vean la fórmula que tenemos acá, ¿qué pasa con esa variable dependiente? ¿Cómo identificarla fácilmente a la hora de un problema? ¿Jóvenes?
E: ¿La dependiente?
P: Sí, la variable dependiente, ¿cómo identificarla?... Vean la fórmula.
E: Di… es el costo de lo que nos van a pedir
P: Es el costo, sí, pero ¿cómo identificar? si yo les doy a ustedes cualquier otra fórmula, ¿cómo pueden identificar ustedes esa variable dependiente? ¿Qué característica tiene ahí? Vean la fórmula, la relación ¿qué pasa con esa variable “C” que es el costo?
E: Es el resultado
E1: Está al lado izquierdo
P: Dicen que está al lado izquierdo, que es el resultado.
E1: Está sola
P: Está solita ¿verdad? entre comillas, eso de estar solita entre comillas ¿qué significa? Que esa variable está ¿qué? Despejada ¿verdad? Vean que está completamente despejada. Entonces es una manera de identificar perfectamente la variable dependiente, es aquella variable que está despejada en la fórmula.
El profesor define los conceptos vistos en clase de forma correcta, tanto de forma oral como en el material de apoyo utilizado [PD].
P: Si todos estos pares ordenados los metemos en un conjunto nuevo es lo que vamos a conocer con el nombre de gráfico de la relación.
P [lee del folleto]: Podemos especificar una relación ya sea gráficamente por medio de diagramas de Venn o bien mediante una lista de pares ordenados que definen la relación, gráfico.
Sobre el vínculo entre conceptos, el docente señala los conceptos variable dependiente y variable independiente. Además, menciona que existe una asociación entre los conceptos relación y función [RR]. Durante la clase, el profesor reconoce, aprovecha y utiliza el contenido matemático de las respuestas adecuadas de sus estudiantes para guiar el proceso de enseñanza [AR].
P: ¿La variable dependiente sería?
E1: “A”
E2: El área
P: El área ¿verdad?, pues el área va a depender del valor que tome ¿quién?, el radio, en este caso “r”. Entonces el área es la variable dependiente por ende “r” sería la variable ¿qué?
E: Independiente
P: Independiente, ¿qué pasa con “Pi” entonces? ¿Será “Pi” una variable?
E1: No
P: ¿Por qué no E1?
E1: Porque “Pi” vale “3,14”
P: “Pi” tiene un valor, ¡excelente! El valor aproximado que le damos a “Pi”, ¿es un valor aproximado de cuánto?
E1: “3,14”
P: “3,14”, ¿eso va a variar en algún momento?
E1: No
P: No, eso va a ser fijo ¿verdad?, recuerden que “Pi” no vale “3,14”, uno usa esa aproximación para cálculos más directos. Ahora bien, entonces si “Pi” no es una variable porque tiene un valor ahí, podemos decir que entonces “Pi” ¿qué es? ¿Una qué? Es un número ustedes me dijeron, entonces ¿”Pi” sería una?
E1: Constante
P: Constante, ¡excelente! “Pi” es una constante, en este caso una constante real, el valor aproximado de “3,14”
Durante el desarrollo de la lección, el docente utiliza correctamente los conceptos correspondientes al tema de funciones y otros conceptos relacionados a este tema [DC].
Episodio [3]
Síntesis del episodio. El profesor hace un repaso de la clase anterior. El estudiantado resuelve ejercicios propuestos en el folleto. Posteriormente, pide a algunos estudiantes ir a la pizarra a escribir las respuestas de los ejercicios.
Conocimientos abarcados. Concepto de función, dominio, codominio, ámbito, relación, diagrama, par ordenado y notación de una función.
Análisis del episodio
El profesor aborda los conceptos correspondientes al programa de estudios y menciona otros conceptos que se relacionan con el tema de funciones [AC].
Para identificar relaciones que corresponden a funciones, el profesor les explica a sus estudiantes un procedimiento para determinarlas [AP].
P: Entonces de ahora en adelante, jóvenes si a ustedes cualquier persona les pregunta ¿qué es una función? Lo primero que van a decir ustedes es una ¿qué?
E: Relación
P: Es una relación, teniendo en cuenta que una relación es una asociación entre elementos de dos conjuntos, como lo decía el compañero anteriormente. Pero una relación que tiene dos condiciones importantes, cada elemento, o sea, todos los elementos de aquí (señala el primer conjunto) tiene que estar relacionado con ¿qué?
E: Un único
P: Un único elemento en el segundo conjunto. Una relación con esta característica es lo que vamos a denominar, entonces, una función entre dos conjuntos.
Los conceptos expuestos por el docente son definidos correctamente durante la lección [PD]. El profesor establece una relación correcta entre los conceptos relación y función [RR]. Sobre las respuestas o intervenciones de sus estudiantes, el profesor reconoce el contenido matemático y lo utiliza para reafirmar conceptos [AR].
P: Ok, le pregunto a E2. ¿Por qué el segundo diagrama no es una función?
E2: Porque no puede tener dos elementos ahí.
P: ¿Quién tiene dos elementos ahí?
E2 : El “3”.
P: El “3” está asociado con dos elementos, ¿qué parte de la definición no cumple? No cumple la palabra...
E: Único
P: Único, ¡excelente!, entonces ya no es una función. Sí, ¡ojo!, y quiero que quede claro, es una relación y aquí podemos concluir algo importante. Toda una función es una ¿qué?, relación, pero no toda relación va a corresponder a una función. Es algo que tienen que manejar siempre.
El profesor utiliza correctamente los conceptos desarrollados en la clase [DC].
Episodio [4]
Síntesis del episodio. El profesor trabaja en la pizarra los conceptos, luego los retoma haciendo uso del folleto. Dicta un problema a los estudiantes para introducir el cálculo de imágenes y preimágenes. El problema trata del salario quincenal de un vendedor de revistas dado por una fórmula donde “y” es el salario percibido y “x” la cantidad de revistas vendidas; destaca el cálculo del salario de acuerdo a la cantidad de revistas vendidas y el cálculo de revistas vendidas para un salario particular. Posteriormente los estudiantes y el profesor hacen la revisión en la pizarra.
Conocimientos abordados. Dominio, codominio, ámbito, preimagen, imagen y criterio de una función.
Análisis del episodio
Durante la lección el docente menciona una diversidad de conceptos propios del tema de funciones y otros relacionados con este [AC]. Cabe destacar que estos conceptos forman parte de unidades temáticas y niveles educativos distintos a los tratados. Si bien, no se hace en este estudio un análisis de los subdominios del Conocimiento del Currículo y Conocimiento en el Horizonte, destacan estas puntualidades en este episodio. Sobre los procedimientos, el profesor enfatiza en estos al abordar los conceptos preimagen, imagen y criterio de una función [AP].
P: Cálculo de imagen es una simple sustitución. Se sustituye la variable independiente por el valor que me estén dando y ya estoy encontrando una imagen.
El profesor define correctamente los conceptos desarrollados en la clase [PD]. También, acentúa las relaciones entre estos conceptos -los presentados en clase- y destaca asociaciones entre conceptos básicos de función con otros conceptos vinculados al tema [RR].
P: Entonces todo par ordenado vamos a tener ya dos nombres, preimagen-imagen, variable independiente-variable dependiente, o también podemos denominar “x”-“y” que más adelante que veamos el plano cartesiano, ya ubicar puntos en el plano cartesiano, siempre se va a mantener este orden “x” coma “y”, primero la preimagen luego la imagen. Por ahí me preguntaba el compañero, que no entendía dos conceptos porque hablaba de formar un par ordenado donde hablaba de abscisa y ordenada, precisamente aquí la variable independiente que es el valor de “x” es la que va a recibir el nombre de abscisa y la otra va a recibir el nombre de ordenada.
El docente reconoce el contenido matemático en las respuestas adecuadas de sus estudiantes, lo aprovecha para reafirmar un concepto y lo utiliza para enriquecer el conocimiento matemático. Por otro lado, reconoce las respuestas inadecuadas de estudiantes y utiliza este contenido para enriquecer el conocimiento matemático [AR].
El profesor utiliza correctamente los conceptos desarrollados y muestra su dominio al responder las preguntas de sus estudiantes en la clase [DC].
Episodio [5]
Síntesis del episodio. El profesor se guía con el folleto y expone los ejemplos en la pizarra.
Conocimientos abordados. Ámbito, preimagen.
Análisis del episodio
El profesor aborda los conceptos básicos de función, incluyendo conceptos fuera de esta temática pero vinculados al tema de funciones [AC].
Sobre los procedimientos, el profesor explica a sus estudiantes cómo calcular la preimagen e imagen y cómo determinar el ámbito de una función [AP].
P: Nos están pidiendo que averigüemos el ámbito de esa función. Ámbito, o sea nos están pidiendo el conjunto de imágenes. Vean que el dominio está compuesto por ¿cuántos elementos?
E: Tres
P: Entonces, por lo tanto, para calcular el ámbito necesito calcular la imagen de cada uno de esos elementos, que va a ser un subconjunto de ¿quién?
E: De los números naturales
P: De los números naturales, o sea que cada una de esas imágenes tiene que ser un número natural
El profesor establece una relación apropiada entre ámbito e imagen [RR]. Reconoce las intervenciones adecuadas de estudiantes, conocimiento matemático que utiliza y aprovecha para reafirmar algún conocimiento [AR].
E: Profe… y digamos, si el número no diera número natural...
P: ¡Ah! Estaríamos en un gran problema, porque entonces la relación ya no sería una función. Eso sería una situación que se pudiera haber presentado si tuviera mal definida la función o la relación. Porque si yo calculo por ejemplo la imagen y no me da un número natural, no podemos decir que esa relación es una función, porque vean que todo el codominio tiene que estar compuesto por números naturales.
Los conceptos utilizados por el docente se emplearon correctamente [DC].
Episodio [6]
Síntesis del episodio. El profesor retoma el contenido del folleto y presenta los ejemplos en la pizarra.
Conocimientos abordados. Función, gráfica.
Análisis del episodio
El profesor menciona conceptos vinculados al concepto función que complementa con otros relacionados con el tema [AC]. Sobre los procedimientos, el docente se centró en explicar a sus estudiantes cómo realizar la gráfica de una función dependiendo de su dominio [AP].
P: Siempre que el dominio este dado por un conjunto finito de elementos la gráfica de la función va a ser únicamente la ubicación de los pares ordenados
El desarrollo de clase se centró en la construcción de la gráfica de la función. El profesor define y utiliza correctamente este concepto [PD]. Además, establece una relación entre gráfico y gráfica [RR].
El docente reconoce las respuestas inadecuadas y aprovecha el contenido matemático de estas para mostrar errores comunes de sus estudiantes al realizar determinados procedimientos [AR]. Asimismo, los conceptos utilizados por el profesor durante la clase se emplearon correctamente [DC].
P: No me vayan a decir como en algún momento un estudiante me dijo “profesor gráfica es el femenino de gráfico”, suena pero no es así ¿verdad?, una cosa es gráfico y la otra cosa es gráfica verdad.
Conclusiones
A partir de la descripción del proceso de enseñanza de un profesor y del análisis de la información se logró observar que el profesor demuestra una amplitud de conceptos relacionados al concepto de función. Incluso mostró dominio de algunos conocimientos que no están incluidos en el programa de estudios oficial para ser abordados en este nivel.
El profesor muestra un dominio y uso correcto de los conceptos básicos de función. Además, incorpora en sus explicaciones conceptos previos y otros que se abordarán en este nivel y en otros niveles, vinculados al tema de funciones. Esto evidencia un conocimiento significativo del programa de estudios para secundaria. Claramente, estos elementos corresponden al subdominio Conocimiento del Currículo, que pone de manifiesto un vínculo entre el Conocimiento del Contenido Matemático y el Conocimiento Pedagógico, en varios momentos de la práctica profesional del profesor cuando enseña los conceptos básicos sobre función.
A pesar de que la temática tratada tiene como punto fuerte la presentación de conceptos y sus significados (conceptos básicos de función), el profesor muestra un uso adecuado de procedimientos para abordar conceptos específicos que admiten una serie de pasos o acciones para su comprensión, como el reconocimiento de relaciones que corresponden a funciones -en distintos modos de representación- y el cálculo de imágenes y preimágenes. Así, se refleja un dominio de conocimiento procedimental adecuado para el abordaje de estos conceptos en secundaria.
Los vínculos entre conceptos planteados permiten identificar una tendencia en el uso de estos vínculos, como la ligazón entre variable independiente y variable dependiente, el enlace entre los conceptos preimagen, criterio de asociación e imagen, y entre gráfico, par ordenado y gráfica de una función. Si bien no se han reconocido la totalidad de los vínculos determinados como unidades de análisis, destaca el uso que hace el profesor de conexiones entre dos o más conceptos durante sus explicaciones.
El profesor tiene una capacidad notable para definir estructuras conceptuales relacionadas a los conceptos básicos de función. Propiamente sobre los conceptos analizados, los conecta para enriquecer el aprendizaje y sostener las estrategias de enseñanza. Esta capacidad trasciende al análisis del Conocimiento Común. El profesor vincula los conceptos estudiados con conceptos previamente desarrollados y con otros que serán presentados en futuras lecciones que forman parte del programa de estudios. Esto resalta el vínculo entre el Conocimiento del Contenido Matemático y el Conocimiento Pedagógico, particularmente para los subdominios del Conocimiento en el Horizonte y el Conocimiento del Currículo.
A pesar de que las intervenciones estudiantiles son escasas -al menos en las sesiones observadas-, el profesor reconoce en estas el contenido matemático de las respuestas adecuadas e inadecuadas y lo aprovecha para reafirmar el significado de los conceptos. De esto, destaca la predisposición de utilizar con frecuencia los aportes de sus estudiantes (contenido matemático) para enriquecer el conocimiento.
Además, se concluye que el profesor demuestra, en sus explicaciones, conocimiento y uso correcto de los conceptos básicos de función: variable independiente y dependiente, relación, función, criterio de asociación, dominio, codominio, preimagen, imagen, ámbito, gráfico, gráfica.
El análisis ha permitido mostrar la pertinencia del procedimiento de investigación realizado para comprender el conocimiento del profesor. Ha posibilitado reconocer en el profesor un número considerable de aspectos sobre el conocimiento común del contenido para la enseñanza de los conceptos básicos de función en cuarto año de la educación secundaria; aspectos que posibilitan caracterizar este conocimiento en el profesor desde el dominio y la amplitud de conceptos matemáticos y sus significados, la relación entre conceptos, el uso de procedimientos matemáticos adecuados durante la clase y la atención al contenido matemático desde las intervenciones de los estudiante.
Esto conduce a una continuidad en la investigación desde los otros tipos de conocimiento con el propósito de tomarlos en consideración para diseñar procesos de formación, inicial o continua, de docentes de matemáticas.
Reconocimientos
Este estudio se ha realizado dentro del proyecto “Conocimiento Matemático para la Enseñanza de las funciones de dos profesores en el Ciclo Diversificado de la Educación Matemática en Costa Rica”, código SIA 0127-13, adscrito a la Escuela de Matemática de la Universidad Nacional de Costa Rica.
Referencias
Badilla, J., Chaves, L., Herrera, D., Morales, Y., Poveda, R., Román, J. y Sánchez, A. (2004). Propuesta didáctica para la enseñanza y aprendizaje de álgebra y funciones: clases tipo taller. (Tesis de Licenciatura). Universidad Nacional, Costa Rica.
Ball, D., Thames, M. y Phelps, G. (2008). Content Knowledge for Teaching: What Makes It Special? Journal of Teacher Education, 59(5), 389-407. doi http://dx.doi.org/10.1177/0022487108324554
Carmona, E. y Climent, N. (2012). Comprensión del conocimiento matemático para la enseñanza que sustenta el diseño de una actividad sobre las ecuaciones de la recta en 1º de Bachillerato. En A. Estepa, Á. Contreras, J. Deulofeu, M. C. Penalva, F. J. García y L. Ordóñez, (Eds.), Investigación en Educación Matemática XVI, 165 - 175. Jaén, España: SEIEM
Carrillo, J., Climent, N., Contreras, L. C. y Muñoz-Catalán, M. C. (2013). Determining spe- cialised knowledge for mathematics teaching. En B. Ubuz, Ç. Haser, M. A. Mariotti, (Eds.), Proceedings of CERME 8[Actas del Octavo Congreso de Investigación europea en Educación Matemática]. Congreso llevado a cabo en Turquía: Middle East Technical University and ERME.
Climent, N. (2002). El desarrollo profesional del maestro de primaria respecto de la enseñanza de la matemática. Un estudio de caso. (Tesis doctoral). Universidad de Huelva, España.
Climent, N. y Carrillo, J. (2003). El dominio compartido de la investigación y el desarrollo profesional. Una experiencia en matemáticas con maestras. Enseñanza de las ciencias: revista de investigación y experiencias didácticas, 21(3), 387-404.
Godino, J. D. (2009). Categorías de análisis de los conocimientos del profesor de matemáticas. UNIÓN, Revista Iberoamericana de Educación Matemática, 20,13-31.
Gómez, P. (2007). Desarrollo del conocimiento didáctico en un plan de formación inicial de profesores de matemáticas de secundaria. (Tesis doctoral). Universidad de Granada, España.
Hill, H., Ball, D. y Schilling, S. (2008). Unpacking Pedagogical Content Knowledge: Conceptualizing and Measuring Teacher’s Topic-Specific Knowledge of Students. Journal for Research in Mathematics Education, 39(4), 372-400.
Lupiañez, J. (2009). Expectativas de aprendizaje y planificación de formación inicial de profesores de matemáticas de secundaria. (Tesis doctoral). Universidad de Granada, España.
McMillan, J. y Schumacher, S. (2005). Investigación educativa. Madrid: Pearson Addison Wesley.
Ministerio de Educación Pública. (2014). Informe nacional 2013. Resultados de las pruebas nacionales de bachillerato de la Educación Formal. Dirección de Gestión y Evaluación de la Calidad. San José, Costa Rica.
Ministerio de Educación Pública. (2012). Programa de Estudios de Matemáticas. Educación General Básica y Ciclo Diversificado. Recuperado de http://www.reformamatematica.net/comunidaded/sites/default/files/programas.pdf
Programa Estado de la Nación en Desarrollo Humano Sostenible (2013). Cuarto Informe Estado de la Educación (4 ed.). San José, Costa Rica: Editorama.
Rico, L. (1997). Los organizadores del currículo de matemáticas. En L. Rico, (Ed.), La educación matemática en la enseñanza secundaria. Barcelona, España: Horsori.
Rico, L. y Fernández-Cano, A. (2013). Análisis didáctico y metodología de investigación. En Rico, L., Lupiáñez, L. y Molina, M. (Eds.), Análisis didáctico en educación matemática. Metodología de investigación, formación de profesores e innovación curricular, 1-22. Granada, España: Comares.
Rojas, N. (2010). Conocimiento para la enseñanza y calidad matemática de la instrucción del concepto de fracción: estudio de caso de un profesor chileno. (Memoria de trabajo de investigación tutelada). Granada, España.
Rojas, N. (2014). Caracterización del conocimiento especializado del profesor de matemáticas: un estudio de casos. Tesis doctoral. Universidad de Granada, España. http://fqm193.ugr.es/produccion-cientifica/tesis/ver_detalles/7483/
Rojas, N., Carrillo, J. y Flores, P. (2012). Características para identificar a profesores de matemáticas expertos. En Estepa, A., Contreras, Á., Deulofeu, J., Penalva, M., García, F. y Ordoñez, L. (Eds.), Investigación en Educación Matemática XVII, 479-485. Jaén, España: SEIEM.
Rojas, N., Flores, P. y Ramos, E. (2013). El análisis didáctico como herramienta para identificar conocimiento matemático para la enseñanza en la práctica. En L. Rico, J. L. Lupiáñez y M. Molina (Eds.), Análisis didáctico en educación matemática. Metodología de investigación, formación de profesores e innovación curricular, 191-208. Granada, España: Comares.
Salcedo, F. (julio-setiembre, 2012). Papel del profesor en la enseñanza de estrategias de aprendizaje. Didasc@lia: Didáctica y Educación, 3(3), 17-28.
Shulman, L. (1986). Those Who Understand: Knowledge growth in Teaching. Educational Researcher, 15(2), 4-14. doi http://dx.doi.org/10.3102/0013189X015002004
Shulman, L. (1987). Knowledge and Teaching: foundations of the New Reform. Harvard Educational Review, 57(1), 1-22. doi http://dx.doi.org/10.17763/haer.57.1.j463w79r56455411
![]()
Conocimiento Común del contenido que manifiesta un profesor al enseñar los conceptos básicos de funciones: un estudio de caso (Ariana Rodríguez-Flores y otros) por Revista Uniciencia se encuentra bajo una Licencia CreativeCommons Atribución-NoComercial-SinDerivadas 3.0 Unported.